Given a Number N
The Fibonacci numbers are the numbers in the following integer sequence.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ……..
In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation
Fn = Fn-1 + Fn-2
with seed values
F0 = 0 and F1 = 1.

Given a number n, print n-th Fibonacci Number.
Examples:
Input : n = 2 Output : 1 Input : n = 9 Output : 34
Write a function int fib(int n) that returns Fn. For example, if n = 0, then fib() should return 0. If n = 1, then it should return 1. For n > 1, it should return Fn-1 + Fn-2
For n = 9 Output:34
Following are different methods to get the nth Fibonacci number.
Method 1 (Use recursion)
A simple method that is a direct recursive implementation mathematical recurrence relation is given above.
C++
#include<bits/stdc++.h>
using namespace std;
int fib( int n)
{
if (n <= 1)
return n;
return fib(n-1) + fib(n-2);
}
int main ()
{
int n = 9;
cout << fib(n);
getchar ();
return 0;
}
C
#include<stdio.h>
int fib( int n)
{
if (n <= 1)
return n;
return fib(n-1) + fib(n-2);
}
int main ()
{
int n = 9;
printf ( "%d" , fib(n));
getchar ();
return 0;
}
Java
class fibonacci
{
static int fib( int n)
{
if (n <= 1 )
return n;
return fib(n- 1 ) + fib(n- 2 );
}
public static void main (String args[])
{
int n = 9 ;
System.out.println(fib(n));
}
}
Python3
def fibonacci(n, second_last, last):
if n - 1 = = 0 :
return second_last
else :
new_last = second_last + last
second_last = last
return fibonacci(n - 1 , second_last, new_last)
if __name__ = = "__main__" :
print (fibonacci( 10 , 0 , 1 ))
C#
using System;
public class GFG
{
public static int Fib( int n)
{
if (n <= 1)
{
return n;
}
else
{
return Fib(n - 1) + Fib(n - 2);
}
}
public static void Main( string [] args)
{
int n = 9;
Console.Write(Fib(n));
}
}
PHP
<?php
function fib( $n )
{
if ( $n <= 1)
return $n ;
return fib( $n - 1) +
fib( $n - 2);
}
$n = 9;
echo fib( $n );
?>
Javascript
<script>
let n = 9;
function fib(n) {
if (n <= 1)
return n;
return fib(n-1) + fib(n-2);
}
document.write(fib(n));
</script>
Time Complexity: Exponential, as every function calls two other functions.
If the original recursion tree were to be implemented then this would have been the tree but now for n times the recursion function is called
Original tree for recursion
fib(5) / \ fib(4) fib(3) / \ / \ fib(3) fib(2) fib(2) fib(1) / \ / \ / \ fib(2) fib(1) fib(1) fib(0) fib(1) fib(0) / \ fib(1) fib(0)
Optimized tree for recursion for code above
fib(5)
fib(4)
fib(3)
fib(2)
fib(1)
Extra Space: O(n) if we consider the function call stack size, otherwise O(1).
Method 2 (Use Dynamic Programming)
We can avoid the repeated work done in method 1 by storing the Fibonacci numbers calculated so far.
C++
#include<bits/stdc++.h>
using namespace std;
class GFG{
public :
int fib( int n)
{
int f[n + 2];
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
{
f[i] = f[i - 1] + f[i - 2];
}
return f[n];
}
};
int main ()
{
GFG g;
int n = 9;
cout << g.fib(n);
return 0;
}
C
#include<stdio.h>
int fib( int n)
{
int f[n+2];
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
{
f[i] = f[i-1] + f[i-2];
}
return f[n];
}
int main ()
{
int n = 9;
printf ( "%d" , fib(n));
getchar ();
return 0;
}
Java
class fibonacci
{
static int fib( int n)
{
int f[] = new int [n+ 2 ];
int i;
f[ 0 ] = 0 ;
f[ 1 ] = 1 ;
for (i = 2 ; i <= n; i++)
{
f[i] = f[i- 1 ] + f[i- 2 ];
}
return f[n];
}
public static void main (String args[])
{
int n = 9 ;
System.out.println(fib(n));
}
}
Python3
def fibonacci(n):
f = [ 0 , 1 ]
for i in range ( 2 , n + 1 ):
f.append(f[i - 1 ] + f[i - 2 ])
return f[n]
print (fibonacci( 9 ))
C#
using System;
class fibonacci {
static int fib( int n)
{
int []f = new int [n + 2];
int i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
{
f[i] = f[i - 1] + f[i - 2];
}
return f[n];
}
public static void Main ()
{
int n = 9;
Console.WriteLine(fib(n));
}
}
PHP
<?php
function fib( $n )
{
$f = array ();
$i ;
$f [0] = 0;
$f [1] = 1;
for ( $i = 2; $i <= $n ; $i ++)
{
$f [ $i ] = $f [ $i -1] + $f [ $i -2];
}
return $f [ $n ];
}
$n = 9;
echo fib( $n );
?>
Javascript
<script>
function fib(n)
{
let f = new Array(n+2);
let i;
f[0] = 0;
f[1] = 1;
for (i = 2; i <= n; i++)
{
f[i] = f[i-1] + f[i-2];
}
return f[n];
}
let n=9;
document.write(fib(n));
</script>
Method 3 (Space Optimized Method 2)
We can optimize the space used in method 2 by storing the previous two numbers only because that is all we need to get the next Fibonacci number in series.
C++
#include<bits/stdc++.h>
using namespace std;
int fib( int n)
{
int a = 0, b = 1, c, i;
if ( n == 0)
return a;
for (i = 2; i <= n; i++)
{
c = a + b;
a = b;
b = c;
}
return b;
}
int main()
{
int n = 9;
cout << fib(n);
return 0;
}
C
#include<stdio.h>
int fib( int n)
{
int a = 0, b = 1, c, i;
if ( n == 0)
return a;
for (i = 2; i <= n; i++)
{
c = a + b;
a = b;
b = c;
}
return b;
}
int main ()
{
int n = 9;
printf ( "%d" , fib(n));
getchar ();
return 0;
}
Java
class fibonacci
{
static int fib( int n)
{
int a = 0 , b = 1 , c;
if (n == 0 )
return a;
for ( int i = 2 ; i <= n; i++)
{
c = a + b;
a = b;
b = c;
}
return b;
}
public static void main (String args[])
{
int n = 9 ;
System.out.println(fib(n));
}
}
Python3
def fibonacci(n):
a = 0
b = 1
if n < 0 :
print ( "Incorrect input" )
elif n = = 0 :
return a
elif n = = 1 :
return b
else :
for i in range ( 2 ,n + 1 ):
c = a + b
a = b
b = c
return b
print (fibonacci( 9 ))
C#
using System;
namespace Fib
{
public class GFG
{
static int Fib( int n)
{
int a = 0, b = 1, c = 0;
if (n == 0) return a;
for ( int i = 2; i <= n; i++)
{
c = a + b;
a = b;
b = c;
}
return b;
}
public static void Main( string [] args)
{
int n = 9;
Console.Write( "{0} " , Fib(n));
}
}
}
PHP
<?php
function fib( $n )
{
$a = 0;
$b = 1;
$c ;
$i ;
if ( $n == 0)
return $a ;
for ( $i = 2; $i <= $n ; $i ++)
{
$c = $a + $b ;
$a = $b ;
$b = $c ;
}
return $b ;
}
$n = 9;
echo fib( $n );
?>
Javascript
<script>
function fib(n)
{
let a = 0, b = 1, c, i;
if ( n == 0)
return a;
for (i = 2; i <= n; i++)
{
c = a + b;
a = b;
b = c;
}
return b;
}
let n = 9;
document.write(fib(n));
</script>
Time Complexity: O(n)
Extra Space: O(1)
Method 4 (Using power of the matrix {{1, 1}, {1, 0}})
This another O(n) which relies on the fact that if we n times multiply the matrix M = {{1,1},{1,0}} to itself (in other words calculate power(M, n)), then we get the (n+1)th Fibonacci number as the element at row and column (0, 0) in the resultant matrix.
The matrix representation gives the following closed expression for the Fibonacci numbers:
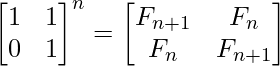
C++
#include<bits/stdc++.h>
using namespace std;
void multiply( int F[2][2], int M[2][2]);
void power( int F[2][2], int n);
int fib( int n)
{
int F[2][2] = { { 1, 1 }, { 1, 0 } };
if (n == 0)
return 0;
power(F, n - 1);
return F[0][0];
}
void multiply( int F[2][2], int M[2][2])
{
int x = F[0][0] * M[0][0] +
F[0][1] * M[1][0];
int y = F[0][0] * M[0][1] +
F[0][1] * M[1][1];
int z = F[1][0] * M[0][0] +
F[1][1] * M[1][0];
int w = F[1][0] * M[0][1] +
F[1][1] * M[1][1];
F[0][0] = x;
F[0][1] = y;
F[1][0] = z;
F[1][1] = w;
}
void power( int F[2][2], int n)
{
int i;
int M[2][2] = { { 1, 1 }, { 1, 0 } };
for (i = 2; i <= n; i++)
multiply(F, M);
}
int main()
{
int n = 9;
cout << " " << fib(n);
return 0;
}
C
#include <stdio.h>
void multiply( int F[2][2], int M[2][2]);
void power( int F[2][2], int n);
int fib( int n)
{
int F[2][2] = {{1,1},{1,0}};
if (n == 0)
return 0;
power(F, n-1);
return F[0][0];
}
void multiply( int F[2][2], int M[2][2])
{
int x = F[0][0]*M[0][0] + F[0][1]*M[1][0];
int y = F[0][0]*M[0][1] + F[0][1]*M[1][1];
int z = F[1][0]*M[0][0] + F[1][1]*M[1][0];
int w = F[1][0]*M[0][1] + F[1][1]*M[1][1];
F[0][0] = x;
F[0][1] = y;
F[1][0] = z;
F[1][1] = w;
}
void power( int F[2][2], int n)
{
int i;
int M[2][2] = {{1,1},{1,0}};
for (i = 2; i <= n; i++)
multiply(F, M);
}
int main()
{
int n = 9;
printf ( "%d" , fib(n));
getchar ();
return 0;
}
Java
class fibonacci
{
static int fib( int n)
{
int F[][] = new int [][]{{ 1 , 1 },{ 1 , 0 }};
if (n == 0 )
return 0 ;
power(F, n- 1 );
return F[ 0 ][ 0 ];
}
static void multiply( int F[][], int M[][])
{
int x = F[ 0 ][ 0 ]*M[ 0 ][ 0 ] + F[ 0 ][ 1 ]*M[ 1 ][ 0 ];
int y = F[ 0 ][ 0 ]*M[ 0 ][ 1 ] + F[ 0 ][ 1 ]*M[ 1 ][ 1 ];
int z = F[ 1 ][ 0 ]*M[ 0 ][ 0 ] + F[ 1 ][ 1 ]*M[ 1 ][ 0 ];
int w = F[ 1 ][ 0 ]*M[ 0 ][ 1 ] + F[ 1 ][ 1 ]*M[ 1 ][ 1 ];
F[ 0 ][ 0 ] = x;
F[ 0 ][ 1 ] = y;
F[ 1 ][ 0 ] = z;
F[ 1 ][ 1 ] = w;
}
static void power( int F[][], int n)
{
int i;
int M[][] = new int [][]{{ 1 , 1 },{ 1 , 0 }};
for (i = 2 ; i <= n; i++)
multiply(F, M);
}
public static void main (String args[])
{
int n = 9 ;
System.out.println(fib(n));
}
}
Python3
def fib(n):
F = [[ 1 , 1 ],
[ 1 , 0 ]]
if (n = = 0 ):
return 0
power(F, n - 1 )
return F[ 0 ][ 0 ]
def multiply(F, M):
x = (F[ 0 ][ 0 ] * M[ 0 ][ 0 ] +
F[ 0 ][ 1 ] * M[ 1 ][ 0 ])
y = (F[ 0 ][ 0 ] * M[ 0 ][ 1 ] +
F[ 0 ][ 1 ] * M[ 1 ][ 1 ])
z = (F[ 1 ][ 0 ] * M[ 0 ][ 0 ] +
F[ 1 ][ 1 ] * M[ 1 ][ 0 ])
w = (F[ 1 ][ 0 ] * M[ 0 ][ 1 ] +
F[ 1 ][ 1 ] * M[ 1 ][ 1 ])
F[ 0 ][ 0 ] = x
F[ 0 ][ 1 ] = y
F[ 1 ][ 0 ] = z
F[ 1 ][ 1 ] = w
def power(F, n):
M = [[ 1 , 1 ],
[ 1 , 0 ]]
for i in range ( 2 , n + 1 ):
multiply(F, M)
if __name__ = = "__main__" :
n = 9
print (fib(n))
C#
using System;
class GFG {
static int fib( int n)
{
int [,]F = new int [,] {{1, 1},
{1, 0} };
if (n == 0)
return 0;
power(F, n-1);
return F[0,0];
}
static void multiply( int [,]F, int [,]M)
{
int x = F[0,0]*M[0,0] + F[0,1]*M[1,0];
int y = F[0,0]*M[0,1] + F[0,1]*M[1,1];
int z = F[1,0]*M[0,0] + F[1,1]*M[1,0];
int w = F[1,0]*M[0,1] + F[1,1]*M[1,1];
F[0,0] = x;
F[0,1] = y;
F[1,0] = z;
F[1,1] = w;
}
static void power( int [,]F, int n)
{
int i;
int [,]M = new int [,]{{1, 1},
{1, 0} };
for (i = 2; i <= n; i++)
multiply(F, M);
}
public static void Main ()
{
int n = 9;
Console.WriteLine(fib(n));
}
}
PHP
<?php
function fib( $n )
{
$F = array ( array (1, 1),
array (1, 0));
if ( $n == 0)
return 0;
power( $F , $n - 1);
return $F [0][0];
}
function multiply(& $F , & $M )
{
$x = $F [0][0] * $M [0][0] +
$F [0][1] * $M [1][0];
$y = $F [0][0] * $M [0][1] +
$F [0][1] * $M [1][1];
$z = $F [1][0] * $M [0][0] +
$F [1][1] * $M [1][0];
$w = $F [1][0] * $M [0][1] +
$F [1][1] * $M [1][1];
$F [0][0] = $x ;
$F [0][1] = $y ;
$F [1][0] = $z ;
$F [1][1] = $w ;
}
function power(& $F , $n )
{
$M = array ( array (1, 1),
array (1, 0));
for ( $i = 2; $i <= $n ; $i ++)
multiply( $F , $M );
}
$n = 9;
echo fib( $n );
?>
Javascript
<script>
function fib( n)
{
var F = [ [ 1, 1 ], [ 1, 0 ] ];
if (n == 0)
return 0;
power(F, n - 1);
return F[0][0];
}
function multiply( F, M )
{
x = F[0][0] * M[0][0] +
F[0][1] * M[1][0];
y = F[0][0] * M[0][1] +
F[0][1] * M[1][1];
z = F[1][0] * M[0][0] +
F[1][1] * M[1][0];
w = F[1][0] * M[0][1] +
F[1][1] * M[1][1];
F[0][0] = x;
F[0][1] = y;
F[1][0] = z;
F[1][1] = w;
}
function power( F, n)
{
var i;
var M = [[ 1, 1 ], [ 1, 0 ]];
for (i = 2; i <= n; i++)
multiply(F, M);
}
var n = 9;
document.write ( " " + fib(n));
</script>
Time Complexity: O(n)
Extra Space: O(1)
Method 5 (Optimized Method 4)
The method 4 can be optimized to work in O(Logn) time complexity. We can do recursive multiplication to get power(M, n) in the previous method (Similar to the optimization done in this post)
C++
#include <bits/stdc++.h>
using namespace std;
void multiply( int F[2][2], int M[2][2]);
void power( int F[2][2], int n);
int fib( int n)
{
int F[2][2] = {{1, 1}, {1, 0}};
if (n == 0)
return 0;
power(F, n - 1);
return F[0][0];
}
void power( int F[2][2], int n)
{
if (n == 0 || n == 1)
return ;
int M[2][2] = {{1, 1}, {1, 0}};
power(F, n / 2);
multiply(F, F);
if (n % 2 != 0)
multiply(F, M);
}
void multiply( int F[2][2], int M[2][2])
{
int x = F[0][0] * M[0][0] + F[0][1] * M[1][0];
int y = F[0][0] * M[0][1] + F[0][1] * M[1][1];
int z = F[1][0] * M[0][0] + F[1][1] * M[1][0];
int w = F[1][0] * M[0][1] + F[1][1] * M[1][1];
F[0][0] = x;
F[0][1] = y;
F[1][0] = z;
F[1][1] = w;
}
int main()
{
int n = 9;
cout << fib(9);
getchar ();
return 0;
}
C
#include <stdio.h>
void multiply( int F[2][2], int M[2][2]);
void power( int F[2][2], int n);
int fib( int n)
{
int F[2][2] = {{1,1},{1,0}};
if (n == 0)
return 0;
power(F, n-1);
return F[0][0];
}
void power( int F[2][2], int n)
{
if ( n == 0 || n == 1)
return ;
int M[2][2] = {{1,1},{1,0}};
power(F, n/2);
multiply(F, F);
if (n%2 != 0)
multiply(F, M);
}
void multiply( int F[2][2], int M[2][2])
{
int x = F[0][0]*M[0][0] + F[0][1]*M[1][0];
int y = F[0][0]*M[0][1] + F[0][1]*M[1][1];
int z = F[1][0]*M[0][0] + F[1][1]*M[1][0];
int w = F[1][0]*M[0][1] + F[1][1]*M[1][1];
F[0][0] = x;
F[0][1] = y;
F[1][0] = z;
F[1][1] = w;
}
int main()
{
int n = 9;
printf ( "%d" , fib(9));
getchar ();
return 0;
}
Java
class fibonacci
{
static int fib( int n)
{
int F[][] = new int [][]{{ 1 , 1 },{ 1 , 0 }};
if (n == 0 )
return 0 ;
power(F, n- 1 );
return F[ 0 ][ 0 ];
}
static void multiply( int F[][], int M[][])
{
int x = F[ 0 ][ 0 ]*M[ 0 ][ 0 ] + F[ 0 ][ 1 ]*M[ 1 ][ 0 ];
int y = F[ 0 ][ 0 ]*M[ 0 ][ 1 ] + F[ 0 ][ 1 ]*M[ 1 ][ 1 ];
int z = F[ 1 ][ 0 ]*M[ 0 ][ 0 ] + F[ 1 ][ 1 ]*M[ 1 ][ 0 ];
int w = F[ 1 ][ 0 ]*M[ 0 ][ 1 ] + F[ 1 ][ 1 ]*M[ 1 ][ 1 ];
F[ 0 ][ 0 ] = x;
F[ 0 ][ 1 ] = y;
F[ 1 ][ 0 ] = z;
F[ 1 ][ 1 ] = w;
}
static void power( int F[][], int n)
{
if ( n == 0 || n == 1 )
return ;
int M[][] = new int [][]{{ 1 , 1 },{ 1 , 0 }};
power(F, n/ 2 );
multiply(F, F);
if (n% 2 != 0 )
multiply(F, M);
}
public static void main (String args[])
{
int n = 9 ;
System.out.println(fib(n));
}
}
Python3
def fib(n):
F = [[ 1 , 1 ],
[ 1 , 0 ]]
if (n = = 0 ):
return 0
power(F, n - 1 )
return F[ 0 ][ 0 ]
def multiply(F, M):
x = (F[ 0 ][ 0 ] * M[ 0 ][ 0 ] +
F[ 0 ][ 1 ] * M[ 1 ][ 0 ])
y = (F[ 0 ][ 0 ] * M[ 0 ][ 1 ] +
F[ 0 ][ 1 ] * M[ 1 ][ 1 ])
z = (F[ 1 ][ 0 ] * M[ 0 ][ 0 ] +
F[ 1 ][ 1 ] * M[ 1 ][ 0 ])
w = (F[ 1 ][ 0 ] * M[ 0 ][ 1 ] +
F[ 1 ][ 1 ] * M[ 1 ][ 1 ])
F[ 0 ][ 0 ] = x
F[ 0 ][ 1 ] = y
F[ 1 ][ 0 ] = z
F[ 1 ][ 1 ] = w
def power(F, n):
if ( n = = 0 or n = = 1 ):
return ;
M = [[ 1 , 1 ],
[ 1 , 0 ]];
power(F, n / / 2 )
multiply(F, F)
if (n % 2 ! = 0 ):
multiply(F, M)
if __name__ = = "__main__" :
n = 9
print (fib(n))
C#
using System;
class GFG
{
static int fib( int n)
{
int [,] F = new int [,]{{1, 1},
{1, 0}};
if (n == 0)
return 0;
power(F, n - 1);
return F[0, 0];
}
static void multiply( int [,] F,
int [,] M)
{
int x = F[0, 0] * M[0, 0] +
F[0, 1] * M[1, 0];
int y = F[0, 0] * M[0, 1] +
F[0, 1] * M[1, 1];
int z = F[1, 0] * M[0, 0] +
F[1, 1] * M[1, 0];
int w = F[1, 0] * M[0, 1] +
F[1, 1] * M[1, 1];
F[0, 0] = x;
F[0, 1] = y;
F[1, 0] = z;
F[1, 1] = w;
}
static void power( int [,] F, int n)
{
if ( n == 0 || n == 1)
return ;
int [,] M = new int [,]{{1, 1},
{1, 0}};
power(F, n / 2);
multiply(F, F);
if (n % 2 != 0)
multiply(F, M);
}
public static void Main ()
{
int n = 9;
Console.Write(fib(n));
}
}
Javascript
<script>
function fib(n)
{
var F = [ [ 1, 1 ], [ 1, 0 ] ];
if (n == 0)
return 0;
power(F, n - 1);
return F[0][0];
}
function multiply(F, M)
{
var x = F[0][0] * M[0][0] + F[0][1] * M[1][0];
var y = F[0][0] * M[0][1] + F[0][1] * M[1][1];
var z = F[1][0] * M[0][0] + F[1][1] * M[1][0];
var w = F[1][0] * M[0][1] + F[1][1] * M[1][1];
F[0][0] = x;
F[0][1] = y;
F[1][0] = z;
F[1][1] = w;
}
function power(F, n)
{
if (n == 0 || n == 1)
return ;
var M = [ [ 1, 1 ], [ 1, 0 ] ];
power(F, n / 2);
multiply(F, F);
if (n % 2 != 0)
multiply(F, M);
}
var n = 9;
document.write(fib(n));
</script>
Time Complexity: O(Logn)
Extra Space: O(Logn) if we consider the function call stack size, otherwise O(1).
Method 6 (O(Log n) Time)
Below is one more interesting recurrence formula that can be used to find n'th Fibonacci Number in O(Log n) time.
If n is even then k = n/2: F(n) = [2*F(k-1) + F(k)]*F(k) If n is odd then k = (n + 1)/2 F(n) = F(k)*F(k) + F(k-1)*F(k-1)
How does this formula work?
The formula can be derived from above matrix equation.
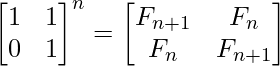
Taking determinant on both sides, we get (-1)n = Fn+1Fn-1 - Fn 2 Moreover, since AnAm = An+m for any square matrix A, the following identities can be derived (they are obtained from two different coefficients of the matrix product) FmFn + Fm-1Fn-1 = Fm+n-1 ---------------------------(1) By putting n = n+1 in equation(1), FmFn+1 + Fm-1Fn = Fm+n --------------------------(2) Putting m = n in equation(1). F2n-1 = Fn 2 + Fn-1 2 Putting m = n in equation(2) F2n = (Fn-1 + Fn+1)Fn = (2Fn-1 + Fn)Fn (Source: Wiki) -------- ( By putting Fn+1 = Fn + Fn-1 ) To get the formula to be proved, we simply need to do the following If n is even, we can put k = n/2 If n is odd, we can put k = (n+1)/2
Below is the implementation of above idea.
C++
#include <bits/stdc++.h>
using namespace std;
const int MAX = 1000;
int f[MAX] = {0};
int fib( int n)
{
if (n == 0)
return 0;
if (n == 1 || n == 2)
return (f[n] = 1);
if (f[n])
return f[n];
int k = (n & 1)? (n+1)/2 : n/2;
f[n] = (n & 1)? (fib(k)*fib(k) + fib(k-1)*fib(k-1))
: (2*fib(k-1) + fib(k))*fib(k);
return f[n];
}
int main()
{
int n = 9;
printf ( "%d " , fib(n));
return 0;
}
Java
import java.util.*;
class GFG {
static int MAX = 1000 ;
static int f[];
public static int fib( int n)
{
if (n == 0 )
return 0 ;
if (n == 1 || n == 2 )
return (f[n] = 1 );
if (f[n] != 0 )
return f[n];
int k = (n & 1 ) == 1 ? (n + 1 ) / 2
: n / 2 ;
f[n] = (n & 1 ) == 1 ? (fib(k) * fib(k) +
fib(k - 1 ) * fib(k - 1 ))
: ( 2 * fib(k - 1 ) + fib(k))
* fib(k);
return f[n];
}
public static void main(String[] args)
{
int n = 9 ;
f= new int [MAX];
System.out.println(fib(n));
}
}
Python3
MAX = 1000
f = [ 0 ] * MAX
def fib(n) :
if (n = = 0 ) :
return 0
if (n = = 1 or n = = 2 ) :
f[n] = 1
return (f[n])
if (f[n]) :
return f[n]
if ( n & 1 ) :
k = (n + 1 ) / / 2
else :
k = n / / 2
if ((n & 1 ) ) :
f[n] = (fib(k) * fib(k) + fib(k - 1 ) * fib(k - 1 ))
else :
f[n] = ( 2 * fib(k - 1 ) + fib(k)) * fib(k)
return f[n]
n = 9
print (fib(n))
C#
using System;
class GFG
{
static int MAX = 1000;
static int [] f;
public static int fib( int n)
{
if (n == 0)
return 0;
if (n == 1 || n == 2)
return (f[n] = 1);
if (f[n] != 0)
return f[n];
int k = (n & 1) == 1 ? (n + 1) / 2
: n / 2;
f[n] = (n & 1) == 1 ? (fib(k) * fib(k) +
fib(k - 1) * fib(k - 1))
: (2 * fib(k - 1) + fib(k)) *
fib(k);
return f[n];
}
static void Main()
{
int n = 9;
f = new int [MAX];
Console.WriteLine(fib(n));
}
}
PHP
<?php
$MAX = 1000;
function fib( $n )
{
global $MAX ;
$f = array_fill (0, $MAX , NULL);
if ( $n == 0)
return 0;
if ( $n == 1 || $n == 2)
return ( $f [ $n ] = 1);
if ( $f [ $n ])
return $f [ $n ];
$k = ( $n & 1) ? ( $n + 1) / 2 : $n / 2;
$f [ $n ] = ( $n & 1) ? (fib( $k ) * fib( $k ) +
fib( $k - 1) * fib( $k - 1)) :
(2 * fib( $k - 1) + fib( $k )) * fib( $k );
return $f [ $n ];
}
$n = 9;
echo fib( $n );
?>
Javascript
<script>
const MAX = 1000;
var f = [...Array(MAX)];
f.fill(0);
function fib(n) {
if (n == 0) return 0;
if (n == 1 || n == 2) return (f[n] = 1);
if (f[n]) return f[n];
var k = n & 1 ? (n + 1) / 2 : n / 2;
f[n] =
n & 1
? fib(k) * fib(k) + fib(k - 1) * fib(k - 1)
: (2 * fib(k - 1) + fib(k)) * fib(k);
return f[n];
}
var n = 9;
document.write(fib(n));
</script>
Time complexity of this solution is O(Log n) as we divide the problem to half in every recursive call.
Method 7
Another approach(Using formula) :
In this method we directly implement the formula for nth term in the fibonacci series.
Fn = {[(√5 + 1)/2] ^ n} / √5
Reference: http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibFormula.html
C++
#include<iostream>
#include<cmath>
int fib( int n) {
double phi = (1 + sqrt (5)) / 2;
return round( pow (phi, n) / sqrt (5));
}
int main ()
{
int n = 9;
std::cout << fib(n) << std::endl;
return 0;
}
C
#include<stdio.h>
#include<math.h>
int fib( int n) {
double phi = (1 + sqrt (5)) / 2;
return round( pow (phi, n) / sqrt (5));
}
int main ()
{
int n = 9;
printf ( "%d" , fib(n));
return 0;
}
Java
import java.util.*;
class GFG {
static int fib( int n) {
double phi = ( 1 + Math.sqrt( 5 )) / 2 ;
return ( int ) Math.round(Math.pow(phi, n)
/ Math.sqrt( 5 ));
}
public static void main(String[] args) {
int n = 9 ;
System.out.println(fib(n));
}
}
Python3
import math
def fibo(n):
phi = ( 1 + math.sqrt( 5 )) / 2
return round ( pow (phi, n) / math.sqrt( 5 ))
if __name__ = = '__main__' :
n = 9
print (fibo(n))
C#
using System;
public class GFG
{
static int fib( int n)
{
double phi = (1 + Math.Sqrt(5)) / 2;
return ( int ) Math.Round(Math.Pow(phi, n)
/ Math.Sqrt(5));
}
public static void Main()
{
int n = 9;
Console.WriteLine(fib(n));
}
}
PHP
<?php
function fib( $n )
{
$phi = (1 + sqrt(5)) / 2;
return round (pow( $phi , $n ) / sqrt(5));
}
$n = 9;
echo fib( $n ) ;
?>
Javascript
<script>
function fib(n) {
let phi = (1 + Math.sqrt(5)) / 2;
return Math.round(Math.pow(phi, n) / Math.sqrt(5));
}
let n = 9;
document.write(fib(n));
</script>
Time Complexity: O(logn), this is because calculating phi^n takes logn time
Space Complexity: O(1)
Method 8
DP using memoization(Top down approach)
We can avoid the repeated work done in method 1 by storing the Fibonacci numbers calculated so far. We just need to store all the values in an array.
C++
#include <bits/stdc++.h>
using namespace std;
int dp[10];
int fib( int n)
{
if (n <= 1)
return n;
int first, second;
if (dp[n - 1] != -1)
first = dp[n - 1];
else
first = fib(n - 1);
if (dp[n - 2] != -1)
second = dp[n - 2];
else
second = fib(n - 2);
return dp[n] = first + second;
}
int main()
{
int n = 9;
memset (dp, -1, sizeof (dp));
cout << fib(n);
getchar ();
return 0;
}
Java
import java.util.*;
class GFG{
static int [] dp = new int [ 10 ];
static int fib( int n)
{
if (n <= 1 )
return n;
int first, second;
if (dp[n - 1 ] != - 1 )
first = dp[n - 1 ];
else
first = fib(n - 1 );
if (dp[n - 2 ] != - 1 )
second = dp[n - 2 ];
else
second = fib(n - 2 );
return dp[n] = first + second;
}
public static void main(String[] args)
{
int n = 9 ;
Arrays.fill(dp, - 1 );
System.out.print(fib(n));
}
}
Python3
dp = [ - 1 for i in range ( 10 )]
def fib(n):
if (n < = 1 ):
return n;
global dp;
first = 0 ;
second = 0 ;
if (dp[n - 1 ] ! = - 1 ):
first = dp[n - 1 ];
else :
first = fib(n - 1 );
if (dp[n - 2 ] ! = - 1 ):
second = dp[n - 2 ];
else :
second = fib(n - 2 );
dp[n] = first + second;
return dp[n] ;
if __name__ = = '__main__' :
n = 9 ;
print (fib(n));
C#
using System;
class GFG {
static int [] dp = new int [10];
static int fib( int n)
{
if (n <= 1)
return n;
int first, second;
if (dp[n - 1] != -1)
first = dp[n - 1];
else
first = fib(n - 1);
if (dp[n - 2] != -1)
second = dp[n - 2];
else
second = fib(n - 2);
return dp[n] = first + second;
}
static void Main()
{
int n = 9;
Array.Fill(dp, -1);
Console.Write(fib(n));
}
}
Javascript
<script>
dp = Array.from({length: 10}, (_, i) => -1);
function fib(n)
{
if (n <= 1)
return n;
var first, second;
if (dp[n - 1] != -1)
first = dp[n - 1];
else
first = fib(n - 1);
if (dp[n - 2] != -1)
second = dp[n - 2];
else
second = fib(n - 2);
return dp[n] = first + second;
}
var n = 9;
document.write(fib(n));
</script>
https://www.youtube.com/watch?v=LwZRsM7qhrI
This method is contributed by Chirag Agarwal.
Method 9 ( Using Binet's Formula for the Nth Fibonacci )
It involves the usage of our golden section number Phi.
Phi = ( sqrt(5) + 1 ) / 2
Using approximation equation is good enough here, since we know N >= 0 && N <= 30, we can safely use the following rounded function
Fib(N) = round( ( Phi^N ) / sqrt(5) )
Full mathematical explanation of Binet's Formula – https://r-knott.surrey.ac.uk/Fibonacci/fibFormula.html
C++
#include<bits/stdc++.h>
using namespace std;
int fib( int n)
{
double phi = ( sqrt (5) + 1) / 2;
return round( pow (phi, n) / sqrt (5));
}
int main()
{
int n = 9;
cout << fib(n);
return 0;
}
Time Complexity: O(1)
Space Complexity: O(1)
Related Articles:
Large Fibonacci Numbers in Java
Please write comments if you find the above codes/algorithms incorrect, or find other ways to solve the same problem.
References:
http://en.wikipedia.org/wiki/Fibonacci_number
http://www.ics.uci.edu/~eppstein/161/960109.html
Source: https://www.geeksforgeeks.org/program-for-nth-fibonacci-number/
0 Response to "Given a Number N"
Post a Comment